吳子青: 影像處理及後製

前言:
常常在攝影的人都知道
用單眼數位拍出來的照片通常需要 “後製”
也就是對照片作修改

因為常常用到像photoimpact或photoshop等的編輯軟體
突然想到可不可以利用
Matlab的強大功能作類似的處理

經過摸索之後找到可以把照片載入matlab的方法
並進行幾項簡單的修改

介紹:

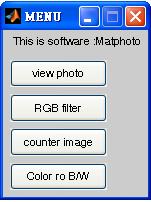
在這裡我選擇了幾項簡單的功能並製作了一個選單
基本的功能包括
1. 觀看原圖 View photo
2. 顏色濾鏡功能 RGB filter
3. 反白 Counter image
4. 彩色照片轉黑白照 Color ro B/W

功能說明：
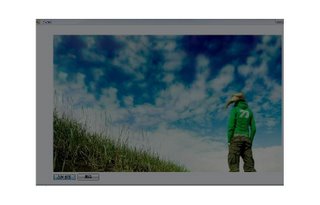
1. View photo
觀看指定的照片 並有放大縮小的功能

2. RGB filter
就像photoshop的濾鏡功能，分成R、G、B 濾鏡
點選之後會輸入三個數值，r、g、b 分別是0~1的數值
1 代表顏色原始呈現 0 代表完全被遮住。

3. Counter image
也就是反白功能，能將明暗對調

4. Color ro B/W
把彩色照片轉換成黑白照片


使用方法：
把想處理的照片 xxx.xxx (如 w.jpg) 放在matlab的 Current Directory。
輸入指令 : Photo
打入 xxx. xx (記得打副檔名)
就進入選單模式

範例：
選這張照片進行處理 “ w.jpg “

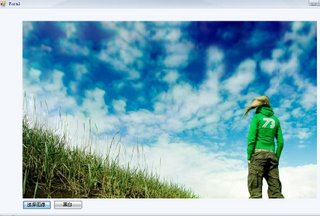
5. (1) View photo
會顯示原照片
http://photos1.blogger.com/x/blogger2/2907/859880749988154/1600/963015/w.jpg

6. (2) RGB filter

R=1
G=0
B=0

http://photos1.blogger.com/x/blogger2/2907/859880749988154/1600/36517/r.jpg

R=0
G=1
B=0

http://photos1.blogger.com/x/blogger2/2907/859880749988154/1600/388570/g.jpg
R=0.5
G=0.5
B=0.5
http://photos1.blogger.com/x/blogger2/2907/859880749988154/1600/500246/05.jpg

R=0
G=1
B=1
http://photos1.blogger.com/x/blogger2/2907/859880749988154/1600/859043/bg.jpg

7. Counter image

http://photos1.blogger.com/x/blogger2/2907/859880749988154/1600/872523/count.jpg

8. Color ro B/W
http://photos1.blogger.com/x/blogger2/2907/859880749988154/1600/673361/gra.jpg

結語：
目前只是最基本的修改功能
未來計畫要加入的包括進接的修改功能及目前富士最新的 臉部辨識功能

程式碼

file=input('select your photo (xxx.xxx)\n:','s');
w=imread(file);
k=menu(' Matphoto v.1 by Ching','View photo','RGB filter','Counter image','Color ro B/W');
switch k
case 1
imview(w);
case 2
r=input('Input your R value(0~1)\n:');
g=input('Input your G value(0~1)\n:');
b=input('Input your B value(0~1)\n:');
w2(:,:,1)=w(:,:,1)*r;
w2(:,:,2)=w(:,:,2)*g;
w2(:,:,3)=w(:,:,3)*b;
imshow(w2);
case 3
w2=256-w;
imshow(w2);
case 4
w2=(w(:,:,1)+w(:,:,2)+w(:,:,3))/3;
imshow(w2);
end

吳子青 本週作業 5.1

-----------------------------------------------------------------
第五章作業5.1 吳子青
R95622024
-----------------------------------------------------------------
Create a 3X3X2 matrix A which contains a matrix of magic(3) and another rand(3,3)*10.
題旨：創造一個多維矩陣，在這裡先宣告 A為 3x3x2矩陣，之後再填入兩個3x3矩陣，分別是 magic(3) 和 rand(3)*10 。

程式內容：
>> A=zeros(3,3,2);
>> A(:,:,1)=magic(3);
>> A(:,:,2)=rands(3,3)*10;
>> A

A(:,:,1) =
8 1 6
3 5 7
4 9 2
A(:,:,2) =
-0.2804 -0.8706 -1.1059
7.8260 -9.6299 2.3086
5.2419 6.4281 5.8387

結果與討論：
結果如上所示，在這裡順便測試一下，當輸入 A(4) 顯示的是 1 ，而
A(12)=5.2419；可以觀察到A(4)=A(1 ,2 ,1)， A(12)= A( 3, 1, 2) 。在多維矩陣裡也可以直接用數列直接呼叫矩陣各個位置，順序為先從 A (: , : , 1)的 第一行、第二行、第三行、A( : , : , 2)的第一行、第二行、第三行。


Assume that matrices A=[45 89 99; 12 34 55], B=[15 25 45; 65 50 30]. Find matrices that join A & B both in vertical and horizontal directions. Also, find a two-page matrix with A & B stored in separate pages. Use commands horizcat and verticat to check the results with those from above.
題旨：
A, B 兩個2x3 矩陣利用 cat 指令作合併的動作，cat(dim ,A ,B)中dim=1
代表兩個矩陣垂直合併，dim=2 代表兩個矩陣平行合併，而dim=3為分頁。
在這裡用dim=1,2,3 分別做出矩陣 C1,C2,C3 ，接著利用 horzcat 指令和vertcat指令檢查，horzcat(A,B) 為平行合併，vertcat(A,B) 為垂直合併。

程式內容
>> A=[45 89 99;12 34 55];
>> B=[15 25 45;65 50 30];
>> C1=cat(1,A,B);
>> C2=cat(2,A,B);
>> C3=cat(3,A,B);
>> C1

C1 =
45 89 99
12 34 55
15 25 45
65 50 30
>> C2
C2 =
45 89 99 15 25 45
12 34 55 65 50 30
>> C3
C3(:,:,1) =
45 89 99
12 34 55
C3(:,:,2) =
15 25 45
65 50 30
>> Ch=horzcat(A,B)
Ch =
45 89 99 15 25 45
12 34 55 65 50 30
>> Cv=vertcat(A,B)
Cv =
45 89 99
12 34 55
15 25 45
65 50 30
>> isequal(Cv,C1)
ans =
1
>> isequal(Ch,C2)
ans =
1
結果與分析
先利用cat(1,A,B) cat(2,A,B) cat(3,A,B) 分別創造平行合併矩陣,垂直合併矩陣,和三維矩陣..C1,C2,C3，可以由程式碼看出結果。而之後用horzcat 和vertcat兩個指令作同樣的動作，為 Ch 和Cv 矩陣，在這裡老師的題目給的指令似乎有筆誤。最後在利用isequal 指令檢查 C1和 Ch是否是相同的矩陣，C2和Cv是否是相同的矩陣，最後結果都是邏輯值 1 ，所以 cat( 1, A, B) = horzcat( A,B)、cat( 2, A, B )=vertcat( A, B) 。

Find a matrix M which contains A as the first and third pages and B the second and fourth pages.
題旨：
已知矩陣 A, B 求M矩陣的第一頁和第三頁是矩陣A，M矩陣的第二頁和第四頁是矩陣B，在這裡可以利用cat指令或是直接宣告 M(: , : , 1)、M(: , : , 2)、M(: , : , 3)、M(: , : , 4)都可以，在這裡採用 cat指令寫成指令檔。

程式內容
/matrix.m/ %matrix的指令檔
function output=matrix(input1,input2)
output=cat(3,input1,input2,input1,input2);

/command windows/ %在command windows執行
舉例來說
>> A=[1 2;3 4];
>> B=[5 6;7 8];
>> M=matrix(A,B);
>> M
M(:,:,1) =
1 2
3 4
M(:,:,2) =
5 6
7 8
M(:,:,3) =
1 2
3 4
M(:,:,4) =
5 6
7 8
結果與分析
在本題試過兩種作法，結果都一樣，一種是用cat(3,A,B) 一種是一頁一頁宣告


Construct a 2X2 cell array that contains 'Eric' [90 100]; 'Peter' [35 60]; 'Jan' [77 67].
題旨：
宣告一個2x3細胞矩陣A包含題目所題到的六個元素，用A(1,1)={}形式設定每個元素的值，再用celldisp把細胞矩陣A的詳細內容展示出來。

程式內容
>> A(1,1)={'Eric'};
>> A(2,1)={'Peter'};
>> A(3,1)={'Jan'};
>> A(1,2)={[90 100]};
>> A(2,2)={[35 60]};
>> A(3,2)={[77 67]};
>> A
A =
'Eric' [1x2 double]
'Peter' [1x2 double]
'Jan' [1x2 double]
>> celldisp(A)
A{1,1} =
Eric
A{2,1} =
Peter
A{3,1} =
Jan
A{1,2} =
90 100
A{2,2} =
35 60
A{3,2} =
77 67

結果與分析
在這裡選用了最基本的指定位置填入內容


Construct a structural Array that contains the following data:Name: 'Philip', 'Peter','Roberts', 'Roe'Age: 35, 45, 55, 60Salary: 50,000 40,000 80,000 120,000

題旨：
宣告一個 結構矩陣，有Name, Age, Salary共三類各4項，在這裡使用指令struct直接宣告內容。

程式內容
>> clear
>> B=struct('Name',{'Philip','Peter','Roberts','Roe'},'Age',{35,45,55,60},'Salary',{'50,000','40,000','80,000','120,000'});

>> B(1)
ans =
Name: 'Philip'
Age: 35
Salary: '50,000'

>> B(2)
ans =
Name: 'Peter'
Age: 45
Salary: '40,000'

>> B(3)
ans =
Name: 'Roberts'
Age: 55
Salary: '80,000'

>> B(4)
ans =
Name: 'Roe'
Age: 60
Salary: '120,000'

結果與分析
使用struct指令可以方便的宣告結構矩陣的內容，免除了一項一項宣告的麻煩，
在struct裡面中括號和大括號的用法需特別注意，如 {35,45,55,60}、[35 45 55 60]、{[35 45 55 60]} 都是不同的結果。

吳子青： 本週作業4.1

1. Two vectors A=3i +5i +10k and B=5i -6j +2k are both passing through an origin. Find the unit vector that is perpendicular to both vectors A & B.

分析：題目要求的是在空間上和A,B兩向量垂直的單位向量，通常作法是取兩向量的外積然後在取單位向量。

程式內容：

clear

A=[3 5 10];

B=[5 -6 2];

c=cross(A,B);

U=c/sqrt(sum(c.^2,2))

U =

0.7511 0.4721 -0.4614

結果與分析：

空間上和A,B兩向量垂直的單位向量 u= (0.7511 ,0.4721 ,-0.4614)

在這裡求向量的長度除了用 sqrt(c*c’) 和 sqrt(dot(c,c))之外的用法

也可以用 sqer(sum(c.^2,2))。

-------------------------------------------------------------------------------------------

2. A=randn(10,10). Find mean(A), median(A,2), std(A), std(A,1,2). Explain the results.

分析：在這裡A是一個10x10的亂數矩陣，在這裡試驗矩陣的一些基礎運算

mean, median,std,std 等，需要注意的地方是dim

程式內容：

A=randn(10,10)

Columns 1 through 5

-0.4326 -0.1867 0.2944 -0.3999 -1.6041

-1.6656 0.7258 -1.3362 0.6900 0.2573

0.1253 -0.5883 0.7143 0.8156 -1.0565

0.2877 2.1832 1.6236 0.7119 1.4151

-1.1465 -0.1364 -0.6918 1.2902 -0.8051

1.1909 0.1139 0.8580 0.6686 0.5287

1.1892 1.0668 1.2540 1.1908 0.2193

-0.0376 0.0593 -1.5937 -1.2025 -0.9219

0.3273 -0.0956 -1.4410 -0.0198 -2.1707

0.1746 -0.8323 0.5711 -0.1567 -0.0592

Columns 6 through 10

-1.0106 0.0000 0.5689 0.6232 0.3899

0.6145 -0.3179 -0.2556 0.7990 0.0880

0.5077 1.0950 -0.3775 0.9409 -0.6355

1.6924 -1.8740 -0.2959 -0.9921 -0.5596

0.5913 0.4282 -1.4751 0.2120 0.4437

-0.6436 0.8956 -0.2340 0.2379 -0.9499

0.3803 0.7310 0.1184 -1.0078 0.7812

-1.0091 0.5779 0.3148 -0.7420 0.5690

-0.0195 0.0403 1.4435 1.0823 -0.8217

-0.0482 0.6771 -0.3510 -0.1315 -0.2656

>> mean(A)

ans =

Columns 1 through 4

0.0013 0.2310 0.0253 0.3588

Columns 5 through 8

-0.4197 0.1055 0.2253 -0.0543

Columns 9 through 10

0.1022 -0.0961

>> median(A,2)

ans =

-0.0933

0.1726

0.3165

0.4998

0.0378

0.3833

0.7561

-0.3898

-0.0197

-0.0953

>> std(A)

ans =

Columns 1 through 5

0.9034 0.8829 1.1898 0.7832 1.0821

Columns 6 through 10

0.8393 0.8575 0.7557 0.7922 0.6292

>> std(A,1,2)

ans =

0.6796

0.8248

0.7283

1.2648

0.8312

0.6643

0.6634

0.7468

1.0275

0.4161

結果與分析：

A是10x10的亂數矩陣，mean(A,dim=1)為從A的每一行取平均，所以結果是1x10矩陣，mean(A)=mean(A,1)相同，dim=1代表取行平均。median(A,2)是從每一列取平均,dim=2代表取列平均，結果為10x1矩陣。 std(A)代表std(A,0,1)預設值 frag=0, dim=1 代表是樣本的標準偏差，自由度＝n-1，取行向量的標準偏差。std(A,1,2) 則是frag=1 代表族群的標準偏差，自由度=n，取列向量的標準偏差，結果為10x1矩陣。

-------------------------------------------------------------------------------------------

3. Prove that exp(i*theta)=cos(theta)+i*sin(theta) using matlab commands.

分析： 利用數值方式證明尤拉公式，因為pi~3.14，所以這裡i=0到10包含所有的狀況，間隔 0.01。A= exp(i*theta)，B= cos(theta)+i*sin(theta)

如果A=B for every theta，show “proved” 尤拉公式得證。

程式內容：

A=zeros(1,1000);

B=zeros(1,1000);

for theta=1:0.01:10

A(1,:)=exp(i*theta);

B(1,:)=cos(theta)+i*sin(theta);

end;

if A-B==0

fprintf('proved!!');

else

fprintf('wrong!');

end

結果與討論：

尤拉公式是複數裡很重要的的定理，要證明要使用幾何的概念，在這裡使用最簡單的方法去證明。

-------------------------------------------------------------------------------------------

4. Let R=eye(3)*5+4*ones(3)i. Find abs(R), angle(R), real(R) and imag(R).

分析：

題目中R是一個複數矩陣，在這裡用兩個矩陣分別是eye和ones組成虛部和實部，然後分別求它的複式平面長度，角度和實部虛部，不過奇怪的是在matlab

裡面直接打eye(3)*5+4*ones(3)I 會顯示錯誤訊息 Error: Missing MATLAB operator.。

程式內容：

A=zeros(3);

A(:)=4i

A =

0 + 4.0000i 0 + 4.0000i 0 + 4.0000i

0 + 4.0000i 0 + 4.0000i 0 + 4.0000i

0 + 4.0000i 0 + 4.0000i 0 + 4.0000i

R=eye(3)*5+A

R =

5.0000 + 4.0000i 0 + 4.0000i 0 + 4.0000i

0 + 4.0000i 5.0000 + 4.0000i 0 + 4.0000i

0 + 4.0000i 0 + 4.0000i 5.0000 + 4.0000i

>> abs(R)

ans =

6.4031 4.0000 4.0000

4.0000 6.4031 4.0000

4.0000 4.0000 6.4031

>> angle(R)

ans =

0.6747 1.5708 1.5708

1.5708 0.6747 1.5708

1.5708 1.5708 0.6747

>> real(R)

ans =

5 0 0

0 5 0

0 0 5

>> imag(R)

ans =

4 4 4

4 4 4

4 4 4

結果與分析：

real 和imag 分別是求複數的實部和虛部，所以答案就是 eye(3)*5 ，是3x3的對角矩陣x5，和ones(3) x4，元素全部是4的3x3矩陣。而abs定義 a+bi à abs=a^2+b^2，就是在複式平面的向量長度，而angle就是向量的角度。

本週作業3.1 吳子青

--------------------------本週作業3.1 吳子青--------------------------
1. for i=1:50, A(i)=i^2; end; A=reshape(A,5,10) Find A. Is there any better way to find the same result?
題旨與分析：由前三行A為1x50的矩陣，元素為從1到50的平方之後經過reshape指令將A轉換為5x10矩陣，而有很多指令或方式可以作矩陣變形的動作，在這裡舉出一些想法。
程式流程與內容：Case 1: 定義每個元素的關係式，利用兩個迴圈跑出5x10的矩陣，為傳統沒有矩陣運算時的方法。 for m=1:5for n=1:10A(m,n)=(5*(n-1)+m)^2;endendclear n;clear m;
Case 2: 先宣告A的大小為5x10矩陣，再利用一個1: 50的迴圈依次填入，用的性質是matlab特有 A( 2,3 )也可用A (5)指定數值的性質
A=zeros(5,10); for i=1:50A(i)=i^2;end;
Case 3: 先做出一從1到50的5x10矩陣，之後在利用點 平方（.^2）直接對矩陣作運算
reshape([1:50],5,10).^2
執行結果：三者都會得到同樣的結果
Columns 1 through 71 36 121 256 441 676 9614 49 144 289 484 729 10249 64 169 324 529 784 108916 81 196 361 576 841 115625 100 225 400 625 900 1225
Columns 8 through 10
1296 1681 21161369 1764 22091444 1849 23041521 1936 24011600 2025 2500
討論：用各種不同的矩陣運算方式都可以得到相同的結果，在這裡就可以見到ｍａｒｌａｂ在矩陣運算強大處
2. Let A=magic(5). Replace the elements that are larger than 10 with 'NaN'
題旨與分析：Ａ＝magic(5)會宣告一個5x5的魔術矩陣，將矩陣裡面大於10的元素以‘NaN’取代，在這裡可以用find指令找到矩陣裡大於10的元素的位置，直接宣告這些位置的元素為NaN
程式流程與內容：A=magic(5);A(find(A>=10))=NaN;A
A =
NaN NaN 1 8 NaN NaN 5 7 NaN NaN 4 6 NaN NaN NaN NaN NaN NaN NaN 3 NaN NaN NaN 2 9
執行結果：A =
NaN NaN 1 8 NaN NaN 5 7 NaN NaN 4 6 NaN NaN NaN NaN NaN NaN NaN 3 NaN NaN NaN 2 9
討論：在A裡面可以直接用算式取代位置變數，相當方便
3. Replace the prime elements in Prob 2 with 0.
題旨與分析：同第二題只是把NaN以0取代
程式流程與內容：
clearA=magic(5);A(find(A>=10))=0;A
A =
0 0 1 8 0 0 5 7 0 0 4 6 0 0 0 0 0 0 0 3 0 0 0 2 9
執行結果：A= 0 0 1 8 0 0 5 7 0 0 4 6 0 0 0 0 0 0 0 3 0 0 0 2 9
討論：在A裡面可以直接用算式取代位置變數，相當方便
4. The function draw_number is shown in sec 3.3. Please make a comparison of results when no_of_draw=[100:100:1000]?
題旨：draw_number 是從0~9取樣n次然後隨機放在5類中，比較取樣100次200次~1000次，看分佈和取樣數目的關係。我想這個題目的重點應該是，怎樣處理能夠讓電腦產生的隨機變數能符合題意所指，也就是10種取樣機率是相同的。
分析：在這裡測試了兩種隨機變數設定圖4-1 fix(rand*10)http://photos1.blogger.com/blogger2/2907/859880749988154/1600/fix.jpg
圖4-2 round(rand*10)http://photos1.blogger.com/blogger2/2907/859880749988154/1600/fix.jpg
從圖4-1可以看到用rand*10產生0~10之間的隨機亂數，用fix正整數化在 0、1、2… 9共10個整數是平均分配，所以符合我們的要求。
程式流程：Step 1：設定 draw_number(no_of_draw) 的function
Step 2：用迴圈從no_of_draw=100跑到1000
程式內容/draw_number.m/function [C]=draw_number(no_of_draw)% draw ball numbers within ndraw times%C=zeros(1,5);n=1;while n<=no_of_draw ball=fix(rand*10); if ball<2 C(1)=C(1)+1; elseif ball<4, C(2)=C(2)+1; elseif ball<6, C(3)=C(3)+1; elseif ball<8, C(4)=C(4)+1; else C(5)=C(5)+1; end n=n+1;end
/command windows/for n=1:10draw(1,n)=draw_number(100*n)end
結果：
22 17 24 18 19 32 36 43 53 36 61 60 52 61 66 92 75 76 82 75 120 94 105 91 90 112 113 113 139 123 146 138 123 153 140 161 154 143 165 177 179 174 185 189 173 190 211 183 208 208討論：因為樣本數太少，所以很難看出選擇方式是否夠逢機，不過從前面的圖上來看，應該是這樣。
5. Please use while...end statement to find out the chances to obtain a preset two-digit number which will be similar to the number set drawn from function rand().
題旨：利用while 和 end的組合寫一個程式，求抽出某一個二位數和電腦亂數選出來的數字相同的機率。
分析：在這裡二位數定義為10~99的數字，我的作法是每個數字亂數投10000次，紀錄當投出來的數字等於某二位數字的累積次數，第一部就是創造一個從10~99可以逢機的亂數，用while指令紀錄累積次數。
程式內容：
clear;clc;P=zeros(1,90);num=[10:99];for N=10:99 m=0; for i=1:10000 while N==fix(rand*89)+10 m=m+1; end; end; P(1,N-9)=m;
end;clear N;clear i;clear m;
結果：10000次的結果http://photos1.blogger.com/blogger2/2907/859880749988154/1600/10000.jpg
100000次的結果http://photos1.blogger.com/blogger2/2907/859880749988154/1600/100000.jpg
1000000次的結果http://photos1.blogger.com/blogger2/2907/859880749988154/1600/1000000.jpg

Matlab作業11/4 Fig